Binero
(Main file name: binero)

The Binero puzzle gives you an N*N grid (N is an even number) in which you have to fill in either a 1 or a 0 at each empty cell. The constraints are the following:

  1. In every row and every column, the number of 1s is equal to the number of 0s.
  2. No three adjacent values may be the same in a row or a column.
  3. No two rows may be identical.
  4. No two columns may be identical.
The following shows an initial grid and a solution.

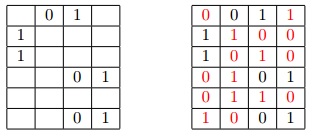
                              binero

Input Formats

An input file for LP systems contains the following facts:
A Minizinc input file specifies the grid size (grid_size), the number of prefilled digits (k),  and three arrays (row, col, and dig) that represent the prefilled digits.

Output format

The output should contain exactly one fact of the form digit(R,C,D) for each cell, where R is the row number, C is the column number, and D is 0 or 1.

Samples


LP InputMinizinc InputOutput
grid_size(6).
digit(1,4,1).
digit(1,5,1).
digit(2,6,0).
digit(3,1,0).
digit(3,3,0).
digit(3,6,1).
digit(4,1,1).
digit(4,3,1).

grid_size = 6;
k = 8;
row = [1,1,2,3,3,3,4,4];
col =   [4,5,6,1,3,6,1,3],
digit = [1,1,0,0,0,1,1,1];
digit(1,1,1).
digit(1,2,0).
digit(1,3,0).
digit(1,4,1).
digit(1,5,1).
digit(1,6,0).
digit(2,1,1).
digit(2,2,0).
digit(2,3,1).
digit(2,4,0).
digit(2,5,1).
digit(2,6,0).
digit(3,1,0).
digit(3,2,1).
digit(3,3,0).
digit(3,4,1).
digit(3,5,0).
digit(3,6,1).
digit(4,1,1).
digit(4,2,0).
digit(4,3,1).
digit(4,4,0).
digit(4,5,0).
digit(4,6,1).
digit(5,1,0).
digit(5,2,1).
digit(5,3,0).
digit(5,4,1).
digit(5,5,1).
digit(5,6,0).
digit(6,1,0).
digit(6,2,1).
digit(6,3,1).
digit(6,4,0).
digit(6,5,0).
digit(6,6,1).
grid_size(6).
digit(1,4,1).
digit(1,5,1).
digit(3,1,0).
digit(3,3,0).
digit(3,6,1).
digit(4,3,1).
digit(5,1,1).
digit(6,6,0).

grid_size = 6;
k = 8;
row = [1,1,3,3,3,4,5,6];
col =  [4,5,1,3,6,3,1,6],
digit = [1,1,0,0,1,1,1,0];		digit(1,1,1).
digit(1,2,0).
digit(1,3,0).
digit(1,4,1).
digit(1,5,1).
digit(1,6,0).
digit(2,1,0).
digit(2,2,1).
digit(2,3,1).
digit(2,4,0).
digit(2,5,0).
digit(2,6,1).
digit(3,1,0).
digit(3,2,1).
digit(3,3,0).
digit(3,4,1).
digit(3,5,0).
digit(3,6,1).
digit(4,1,1).
digit(4,2,0).
digit(4,3,1).
digit(4,4,0).
digit(4,5,1).
digit(4,6,0).
digit(5,1,1).
digit(5,2,0).
digit(5,3,1).
digit(5,4,0).
digit(5,5,0).
digit(5,6,1).
digit(6,1,0).
digit(6,2,1).
digit(6,3,0).
digit(6,4,1).
digit(6,5,1).
digit(6,6,0).
grid_size(8).
digit(1,4,1).
digit(1,7,1).
digit(3,1,0).
digit(3,3,0).
digit(3,6,1).
digit(4,3,1).
digit(5,1,1).
digit(6,6,0).
digit(8,7,1).

grid_size = 8;
k = 9;
row = [1,1,3,3,3,4,5,6,8];
col =  [4,7,1,3,6,3,1,6,7],
digit = [1,1,0,0,1,1,1,0,1];		digit(1,1,1).
digit(1,2,0).
digit(1,3,0).
digit(1,4,1).
digit(1,5,0).
digit(1,6,1).
digit(1,7,1).
digit(1,8,0).
digit(2,1,0).
digit(2,2,1).
digit(2,3,1).
digit(2,4,0).
digit(2,5,1).
digit(2,6,0).
digit(2,7,0).
digit(2,8,1).
digit(3,1,0).
digit(3,2,1).
digit(3,3,0).
digit(3,4,1).
digit(3,5,0).
digit(3,6,1).
digit(3,7,0).
digit(3,8,1).
digit(4,1,1).
digit(4,2,0).
digit(4,3,1).
digit(4,4,0).
digit(4,5,1).
digit(4,6,0).
digit(4,7,1).
digit(4,8,0).
digit(5,1,1).
digit(5,2,1).
digit(5,3,0).
digit(5,4,0).
digit(5,5,1).
digit(5,6,1).
digit(5,7,0).
digit(5,8,0).
digit(6,1,0).
digit(6,2,1).
digit(6,3,0).
digit(6,4,1).
digit(6,5,0).
digit(6,6,0).
digit(6,7,1).
digit(6,8,1).
digit(7,1,1).
digit(7,2,0).
digit(7,3,1).
digit(7,4,1).
digit(7,5,0).
digit(7,6,1).
digit(7,7,0).
digit(7,8,0).
digit(8,1,0).
digit(8,2,0).
digit(8,3,1).
digit(8,4,0).
digit(8,5,1).
digit(8,6,0).
digit(8,7,1).
digit(8,8,1).