| LP Input | Minizinc Input | Output |
| graph_size(6). start(1). dest(6). edge(1,2,4). edge(1,3,2). edge(2,3,5). edge(2,4,10). edge(3,5,3). edge(4,5,4). edge(4,6,11). | graph_size = 6; start = 1; n_dests = 1; dest = [6]; n_edges = 7; from = [1,1,2,2,3,4,4]; to = [2,3,3,4,5,5,6]; cost = [4,2,5,10,3,4,11]; | min_cost(20). |
| graph_size(6). start(1). dest(5). dest(6). edge(1,2,4). edge(1,3,2). edge(2,3,5). edge(2,4,10). edge(3,5,3). edge(4,5,4). edge(4,6,11). | graph_size = 6; start = 1; n_dests = 2; dest = [5,6]; n_edges = 7; from = [1,1,2,2,3,4,4]; to = [2,3,3,4,5,5,6]; cost = [4,2,5,10,3,4,11]; | min_cost(20). |
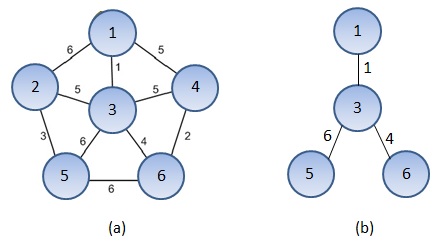
| graph_size(6). start(1). dest(5). dest(6). edge(1,2,6). edge(1,3,1). edge(1,4,5). edge(2,3,5). edge(2,5,3). edge(3,4,5). edge(3,5,6). edge(3,6,4). edge(4,6,2). | graph_size = 6; start = 1; n_dests = 2; dest = [5,6]; n_edges = 9; from = [1,1,1,2,2,3,3,3,4]; to = [2,3,4,3,5,4,5,6,6]; cost = [6,1,5,5,3,5,6,4,2]; | min_cost(11). |